選択した画像 二 等辺 三角形 比 280733

 今、二等辺三角形が熱い！ ～小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学 頂角36度の二等辺三角形の頂点を同じ位置にして、10個並べると正10角形になります。 この正10角形に外接する円の半径（二等辺の長さ）と 正10角形の辺の長さ（二等辺三角形の底辺の長さ）の比を黄金比と言います。 その比は、二等辺三角形の底辺の長さ二等辺三角形（にとうへんさんかくけい、英 isosceles triangle ）は、三角形の一種で、3 本の辺のうち（少なくとも）2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

二 等辺 三角形 比

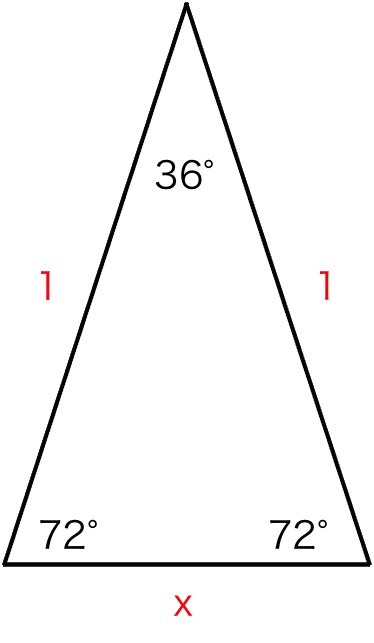
二 等辺 三角形 比- 36度の三角比 次の図は、 $\mathrm{ AB }=\mathrm{ AC }$ の二等辺三角形 ABC をかいたものです。 $\angle \mathrm{ A }=36^{\circ}$ で、 $\mathrm{ BC }=1$ とします。今、 $\mathrm{ AB }=x$ とおいて、これを求めてみましょう。これがわかると、36度の三角比も求められるようになりAE＝AC －④ の二等辺三角形であることがわかる。 （※ ※2つの角が等しい三角形は二等辺三角形 ） 次にADとECは平行であるので BD：DC＝BA：AE －⑤ （※ 平行線と線分の比 ） ④と⑤より BD：DC＝AB：AC が成り立つことがわかる。

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

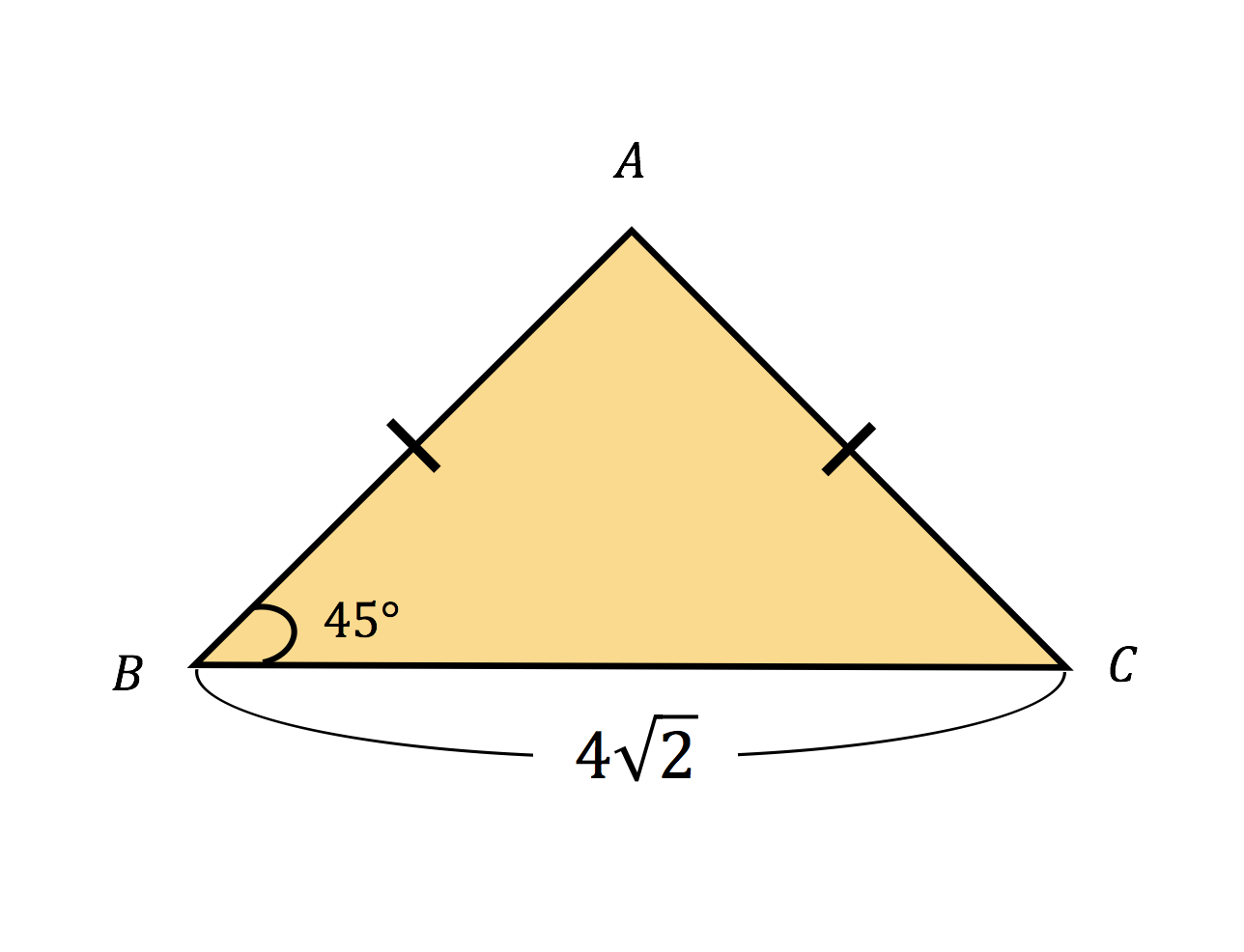
それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、よく利用することになるので覚えておきましょう。 30°、60°、90°の直角三角形→辺の長さの比は\(1：2：\sqrt{3}\) 三角形の辺の長さの比が\(1：2：\sqrt{3}\)→ 30°、60°、90°の直角三角形 二等辺三角形ではない三角形を思い浮かべてください。 いろんな三角形が思い浮かんだと思いますが、その中に正三角形はありましたか？ ないですよね？ すなわち 二等辺三角形ではない ならば 正三角形ではない これは今、想像してもらった通り真です。直角二等辺三角形の定規の辺の比は、11 √2（内角は、90°、45°、45°） この場合、斜辺が√2です。 1² ＋ 1² =√2² また、直角二等辺三角形といえば、正方形を対角線で半分に切った図形です。

三角形と比の定理 したがって efgは二等辺三角形となる。 確認 四角形abcdで、p,rはそれぞれ辺ad, bcの中点、q,sはそれぞれ対角線bd,acの中点である。 答表示 a b 小学生レベルでの直角二等辺三角形の底辺の長さの求め方が解りません中学生レベルであれば√を使って求められますが 小学生では、？解られる方教えて下さい。#5です。小学生レベルでの似たような問題で「面積が 25cm^2 の直角二等辺三角 まとめ：二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく 底辺の半分の長さを求める そいつを2倍する っていう3ステップでいいんだ。 どんどん問題をといてみよう！ そんじゃねー Ken

 二等辺三角形の一辺から 直角に線 を引き、 高さ を作ります。 高さの長さを求める 補助線により出来た三角形は、 30°, 60°, 90°の直角三角形 です。 この 三角形は 一番長い辺と一番短い辺の 長さの比が 2 1 になっています。二等辺三角形の高さの求め方 まとめ 二等辺三角形の高さを求めるためには まず、頂角からまっすぐな線を引きましょう！ すると、直角三角形を作ることができるので そこから三平方の定理を使ったり 角度がわかる場合には比を取って 高さを求めてき 次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。

今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかここまでで、線分比について次の3つのヒントが集まったね。 ① aq：qc＝ab：cb ② ap：pb＝ac：bc ③ ap：pb＝aq：qc つなげて考えると、 ab：cb＝ac：bc となるね。ここで、bcは共通だから、 ab＝ac が言える。つまり、 abcの正体は 「ab=acの二等辺三角形」 なんだ。直角二等辺三角形の特徴は、 ・辺の長さの比が「1：1：√2」 ・角度が45度 である点です。 上記は是非覚えてください。 下記も参考になります。 直角二等辺三角形と三平方の定理の関係は？ 3分でわかる計算、公式、辺の比、例題

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

よく使う三角比の値 数学i By Okボーイ マナペディア

使用目的 工作機械でV字刃物を使う際の設計で利用しました。 様々な条件でぱっと計算してくれるので大変助かります。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 二等辺三角形 のアンケート記入欄 年齢 歳未満 歳 要点 二等辺三角形の定義：2つの辺が等しい三角形 二等辺三角形の性質①：二等辺三角形の2つの底角は等しい 二等辺三角形の性質②：二等辺三角形の頂角の二等分線は底辺を垂直に2等分する 二等辺三角形の性質を利用した角度の問題（基礎編）辺の長さの比1：1：1 直角二等辺三角形です。 直角をはさむ2辺の長さは同じ です。 辺の長さの比1：1：√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。 辺の長さの比1：2：√3 3辺の比が簡単な整数となる直角

三角比 30 45 60 もう一度やり直しの算数 数学

タンジェントとは何か 中学生でも分かる三角関数の基礎

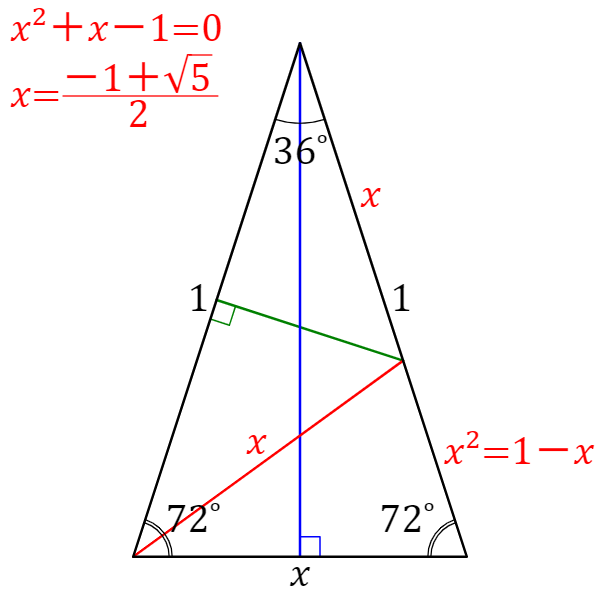
二等辺三角形を見つけることができるので、それをたどっていくと、\(AB=x1\) と表せますね。 これを用いて相似比をとっていくと、次のように \(x\) を求めることができます。さて，36度の三角比を求めるには，この形の中の acdを使う． つまり頂角36度，底角72度の二等辺三角形である． まず底角cの2等分線を引く．（正5角形の対角線ceにあたる） その線とadとの交点をqとすると， qacはa=c=36度の二等辺三角形である．直角二等辺三角形（ちょっかくにとうへんさんかくけい、英 isosceles right triangle ）は、二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形である。 3つの角のうち2つの角がそれぞれ45°である三角形と定義してもよい。 直角二等辺三角形は二等辺三角形の一つでもあり、直角

三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写 Clearnote

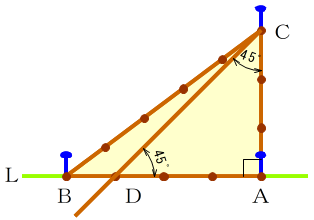
３ ４ ５の三角形で 本当に直角ができる Note Board

$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。は黄金比φ 2 5 1 の逆数 であるから，内接円の半径が最大となると き，等辺：底辺 φ：2 である．黄金比が 最も美しい比であると言われるが，それに 倣えばこの比の二等辺三角形が最も美し い二等辺三角形であると言えるのだろうか．確かに，安定感を送信を完了しました。 直角二等辺三角形 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

二等辺三角形の分割

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

Qv4jlk Y10j7gm

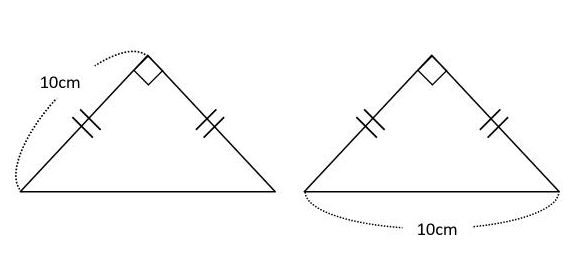
二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

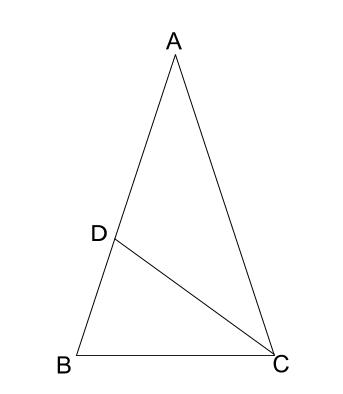
中学数学 相似と方程式 中学数学の無料オンライン学習サイトchu Su

数学ルート斜辺が１０cmの直角二等辺三角形の周の長さを求めなさい答１０ Yahoo 知恵袋

3

二等辺三角形 Wikipedia

黄金三角形による18 シリーズの三角比 おいしい数学

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア

高校入試 英語 数学 特別な直角三角形

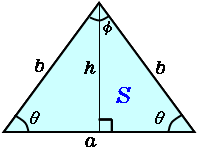
二等辺三角形 高精度計算サイト

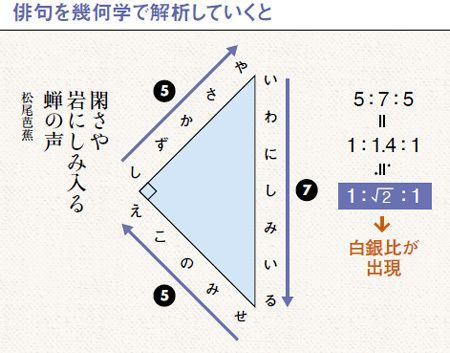
5 7 5 の俳句に隠されていた 白銀比 2ページ目 President Online プレジデントオンライン

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

18 36 72 などの三角比 5角形 10角形 黄金比 社会人になってからのスキルアップ

Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

二等辺三角形の分割

直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題

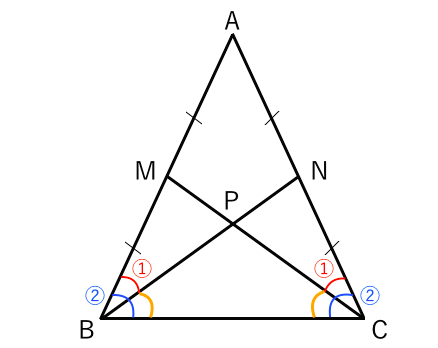
合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に

Sin Cos Tan で手計算で計算できるものまとめ 数学の偏差値を上げて合格を目指す

三角比を考え方から理解する 有名角の三角比も説明

連続する二等辺三角形の角度の法則 算数解法の極意

3

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

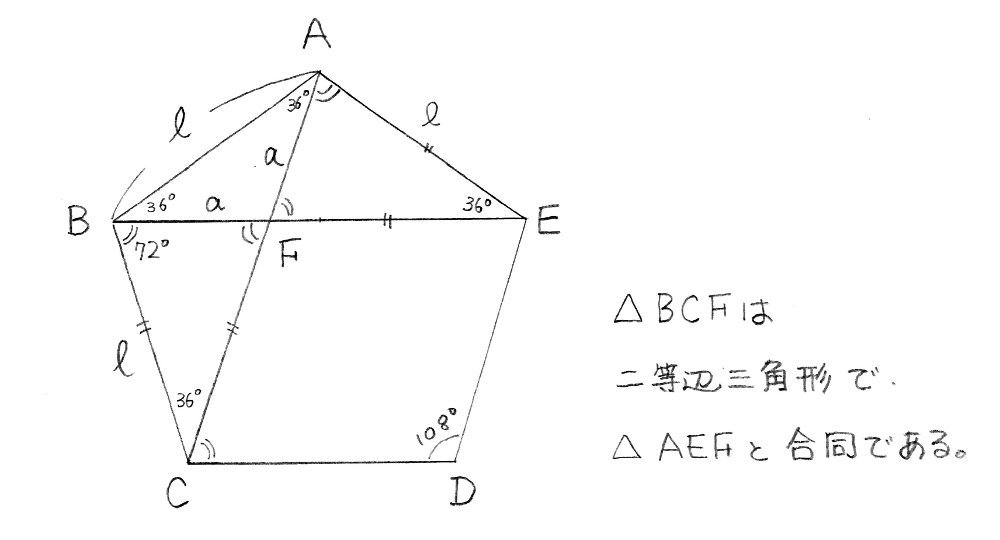
五角形５ 辺と対角線の比 Wandering In The Woods

この公式は角度が1のときだけ使えるのですか Clearnote

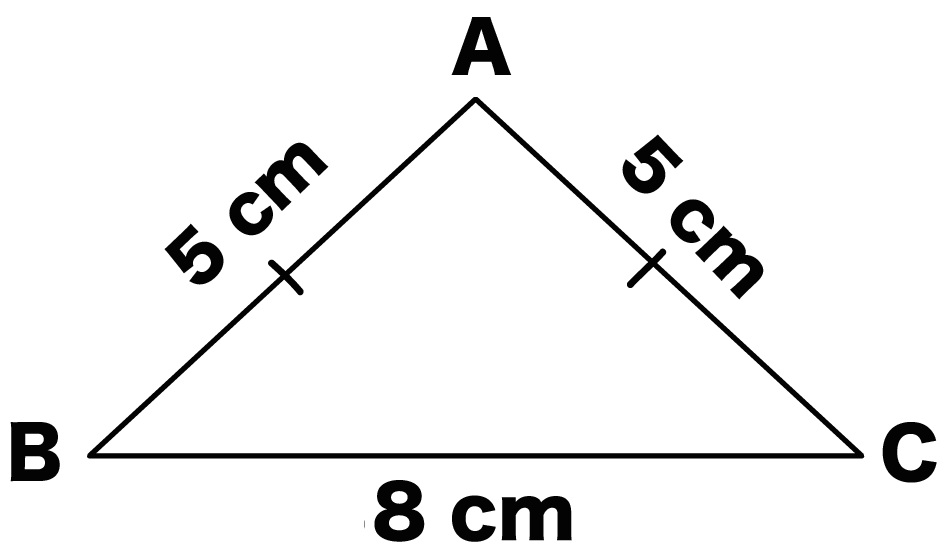
簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

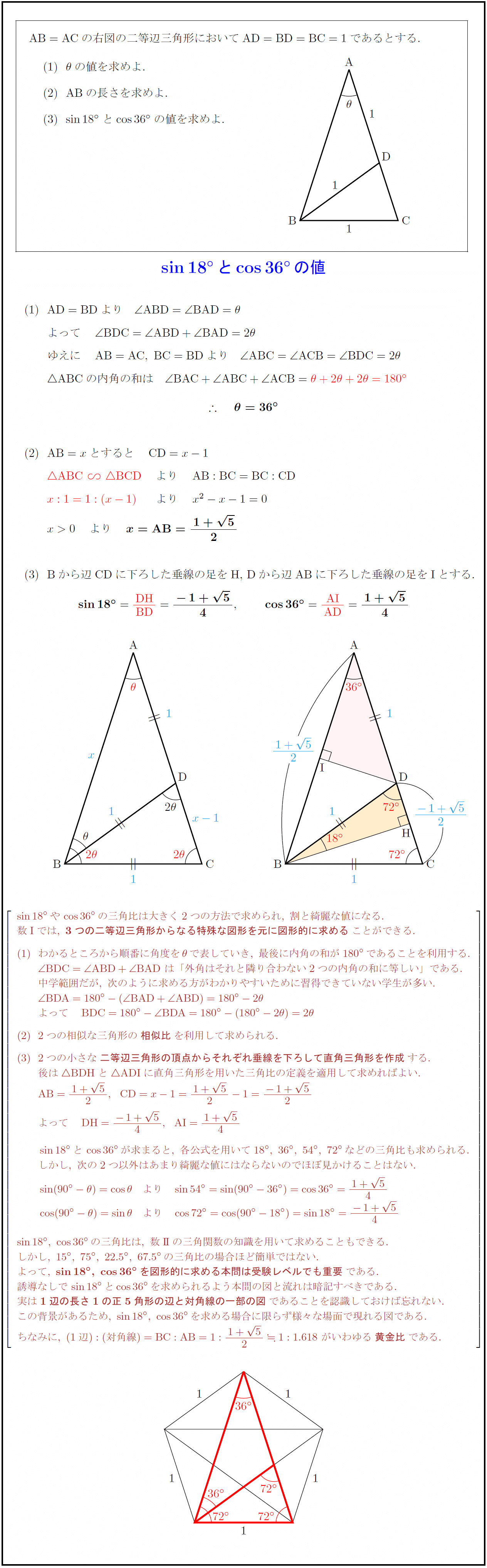
高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

スタディピア 図形

白銀比三角形を見ていて気付いたこと 大したことない Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー

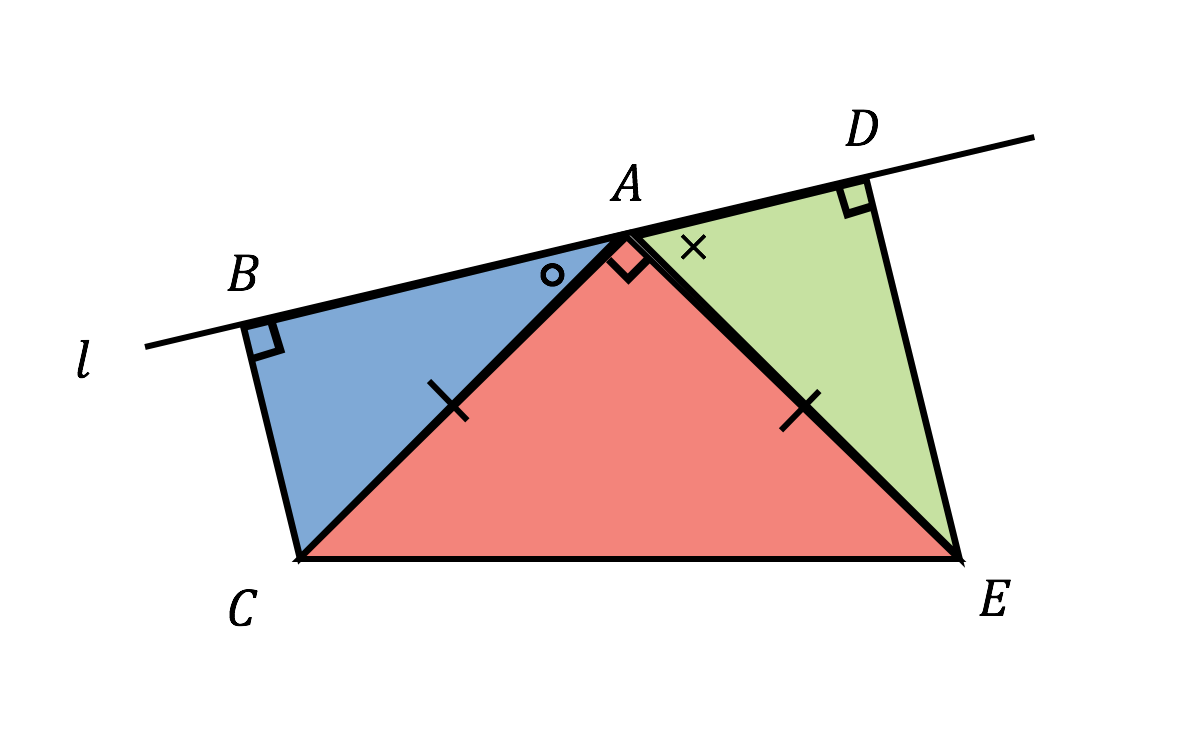
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

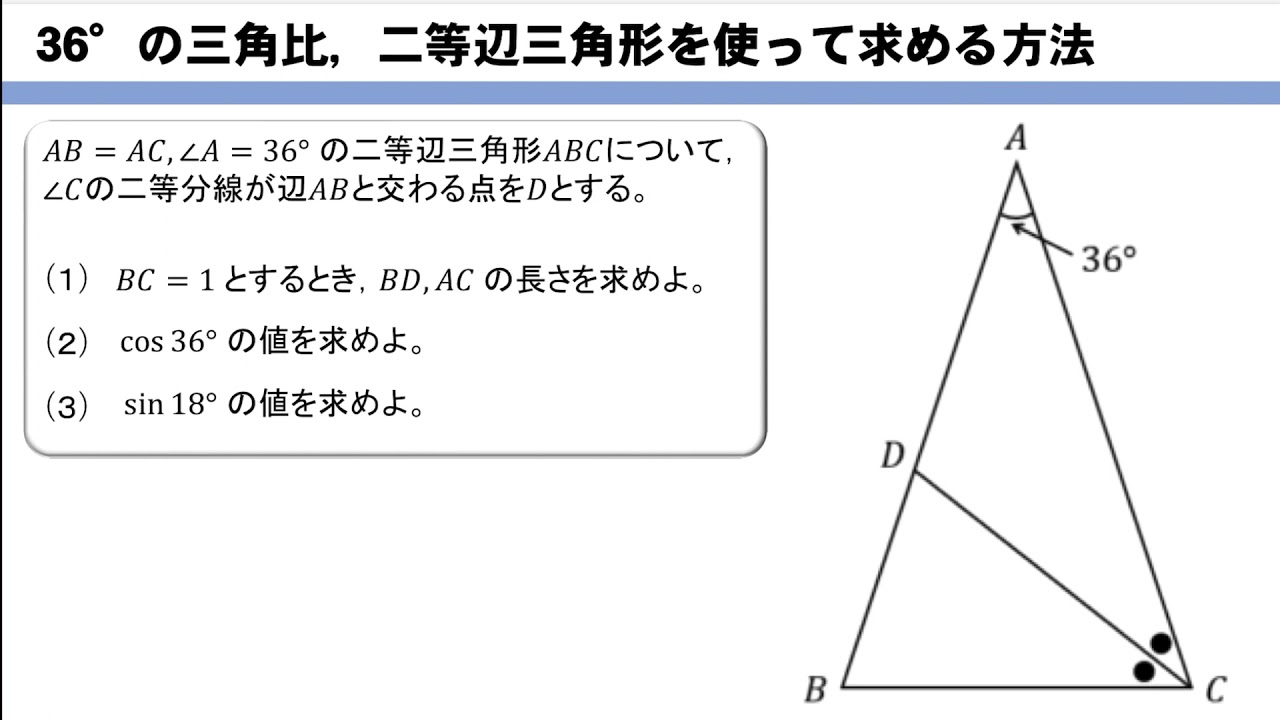
36 の三角比 二等辺三角形を用いて求める方法は Youtube

円に内接 外接する正方形の周の長さを計算してみる 数学について考えてみる

数学の質問です ルート2はどこから分かるんですか 直角二等辺三角 Yahoo 知恵袋

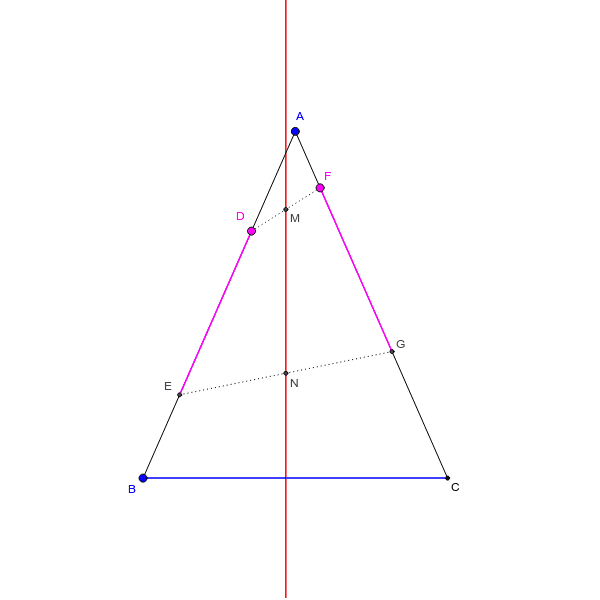
二等辺三角形と垂線 Geogebra

特別な直角三角形の辺の比 無料で使える中学学習プリント

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

応用 36度の三角比 なかけんの数学ノート

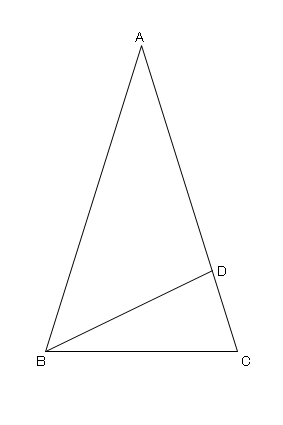
三角形の相似の証明 2 ネット塾

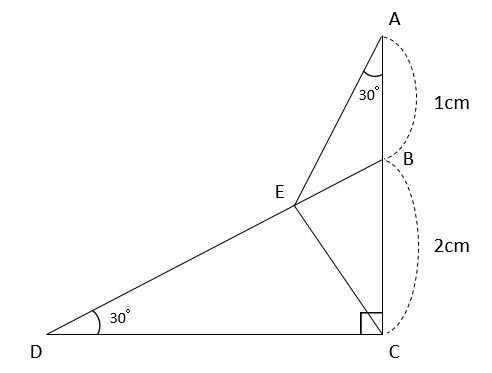
相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

二等辺三角形の面積を求める算数の公式は

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月

三角形の面積 中学受験 塾なし の勉強法

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

二等辺三角形 ゆるゆるプログラミング

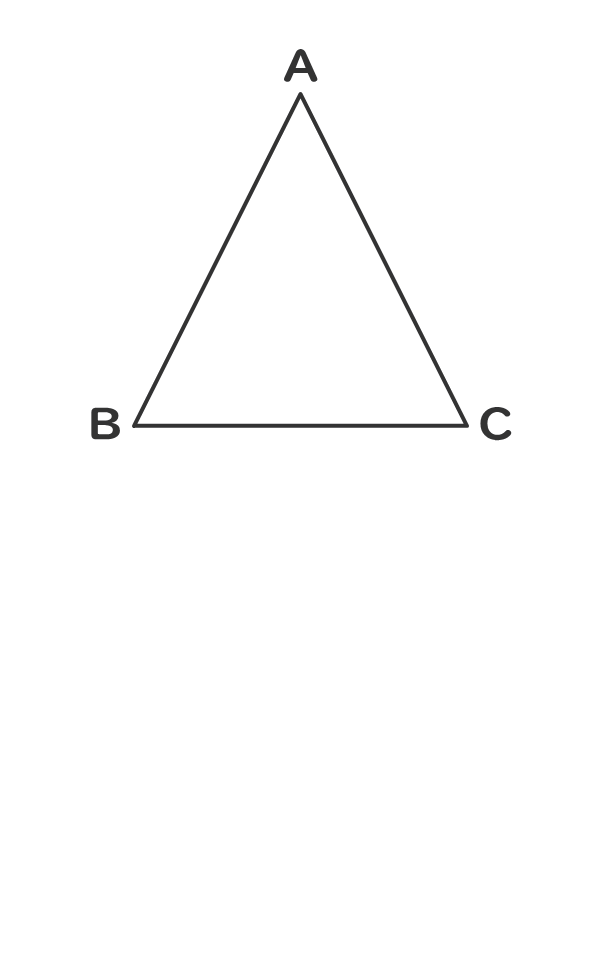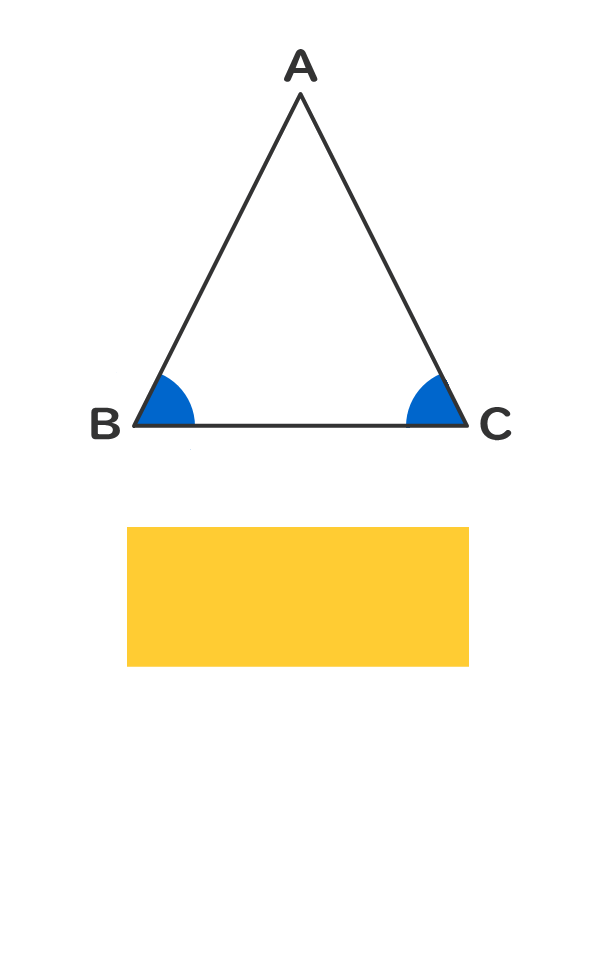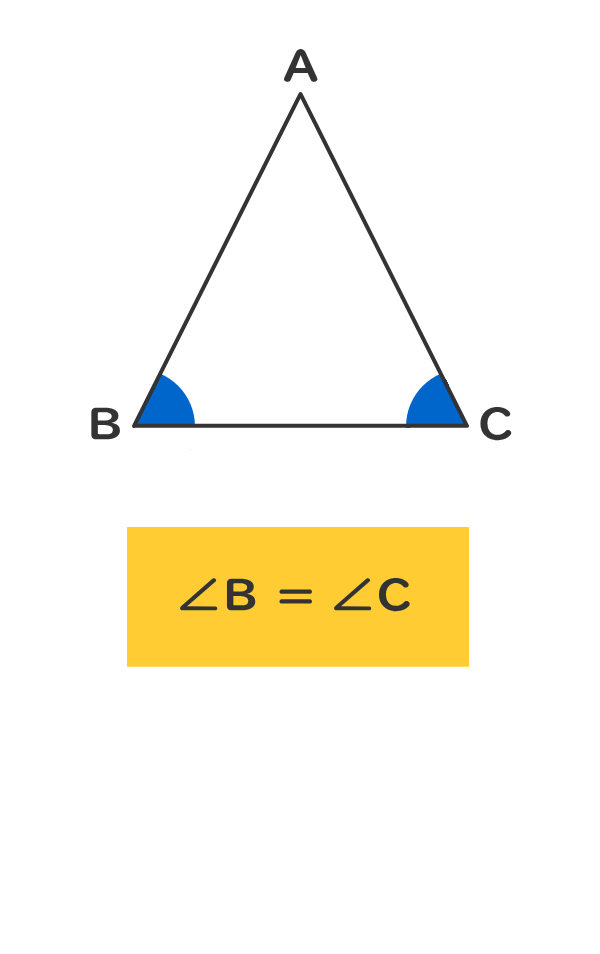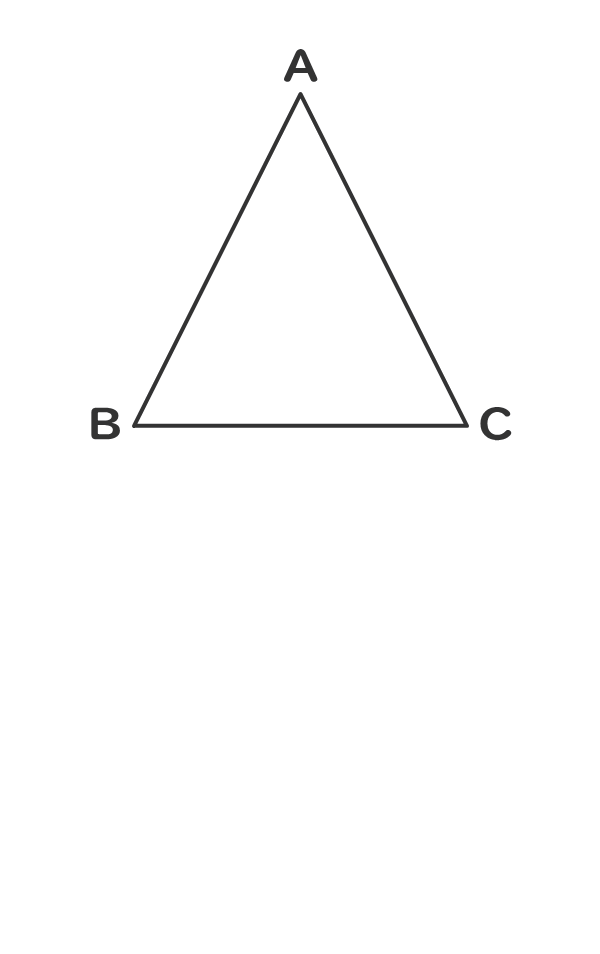
三角形の種類を判定しよう 電験3種web

黄金比と正面体

なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてくだ Clearnote

この二等辺三角形の角度を求めてください この三角形は Ab Acの二等辺 Okwave

南山中学女子部過去問題演習

黄金三角形による18 シリーズの三角比 おいしい数学

1

くろべえ 18 36 54 72 の三角比 Sin Cos

1

100 Ou Plus 直角二等辺三角形 比率 直角二等辺三角形 比率

標準 ベクトルの内積と二等辺三角形 なかけんの数学ノート

黄金三角形による18 シリーズの三角比 おいしい数学

数学の内心の問題です 1 1 2の比の直角三角形の内接円の半径が1セン 数学 教えて Goo

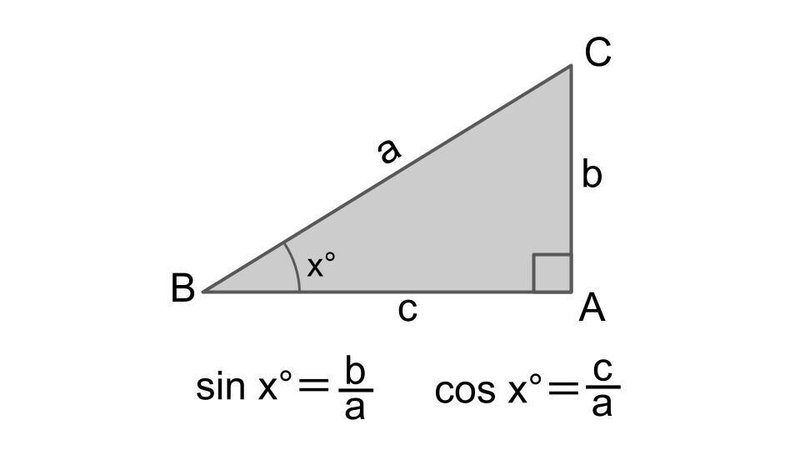
三角関数とは Part1 三角比 Sin Cosとは Toy Note

２ 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に

36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext

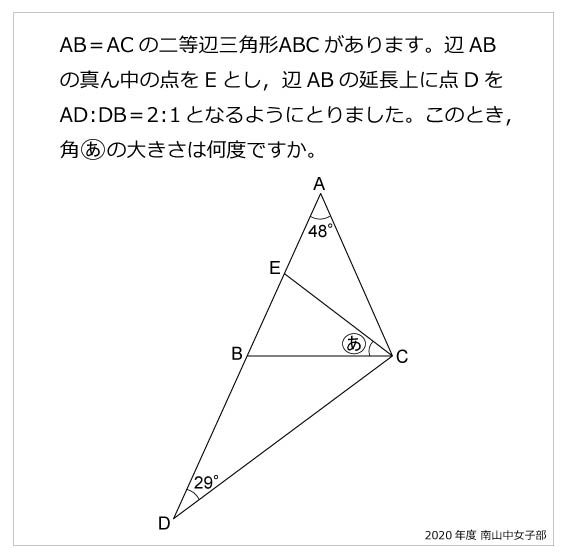
二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦

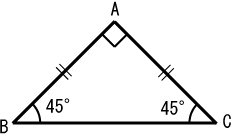
直角二等辺三角形 Wikipedia

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

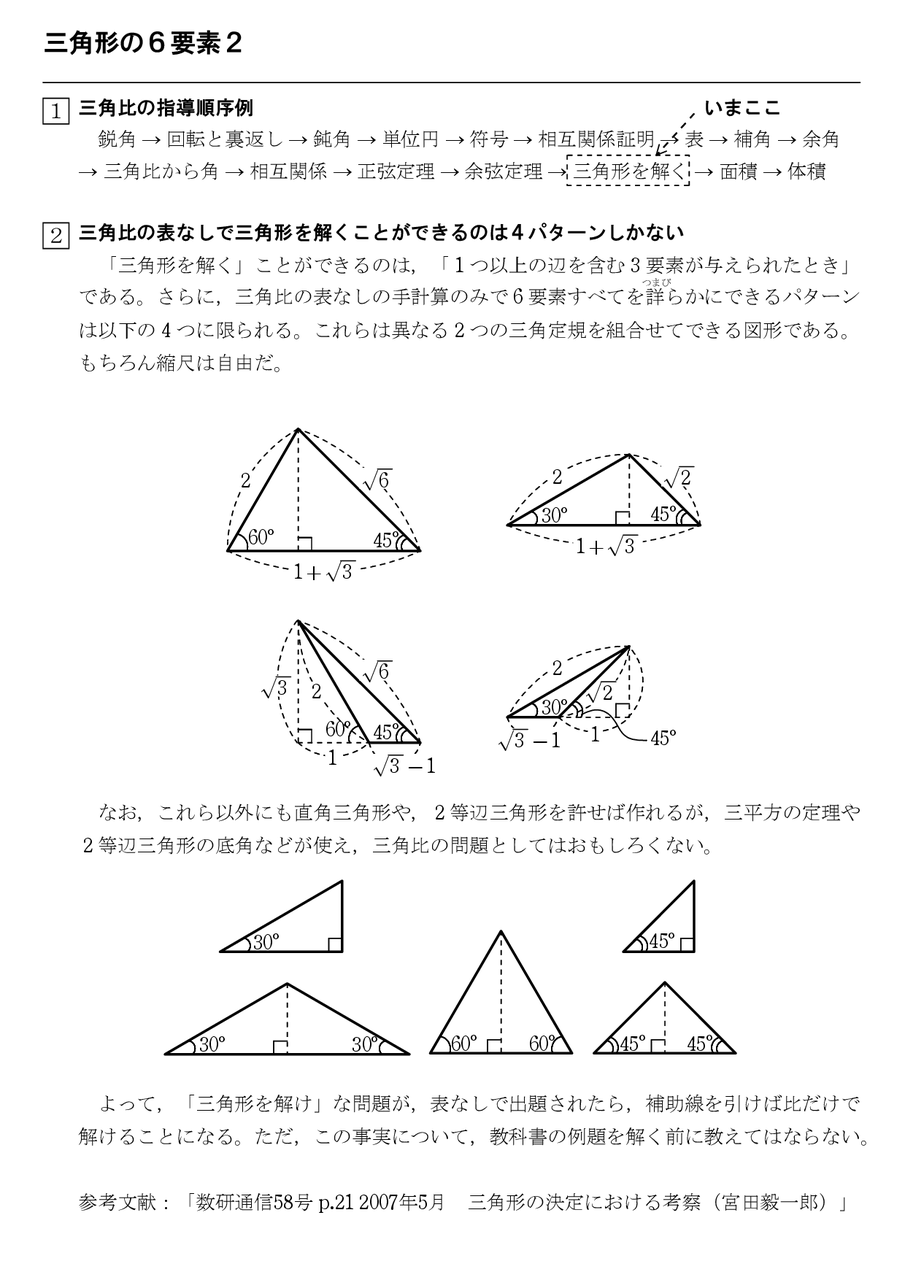
三角形の６要素２ 怜悧玲瓏 高校数学を天空から俯瞰する

直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう

角の二等分線の性質と二等分線の長さ 思考力を鍛える数学

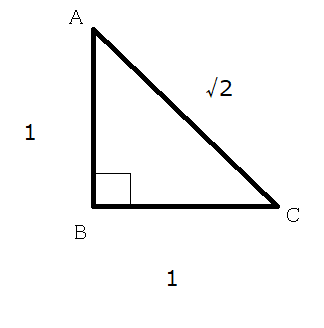
三角関数が大事だという話 Wawabubu なおぼん のblog

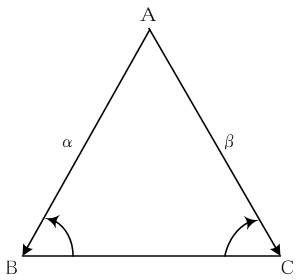
3 2 三角形とベクトル比

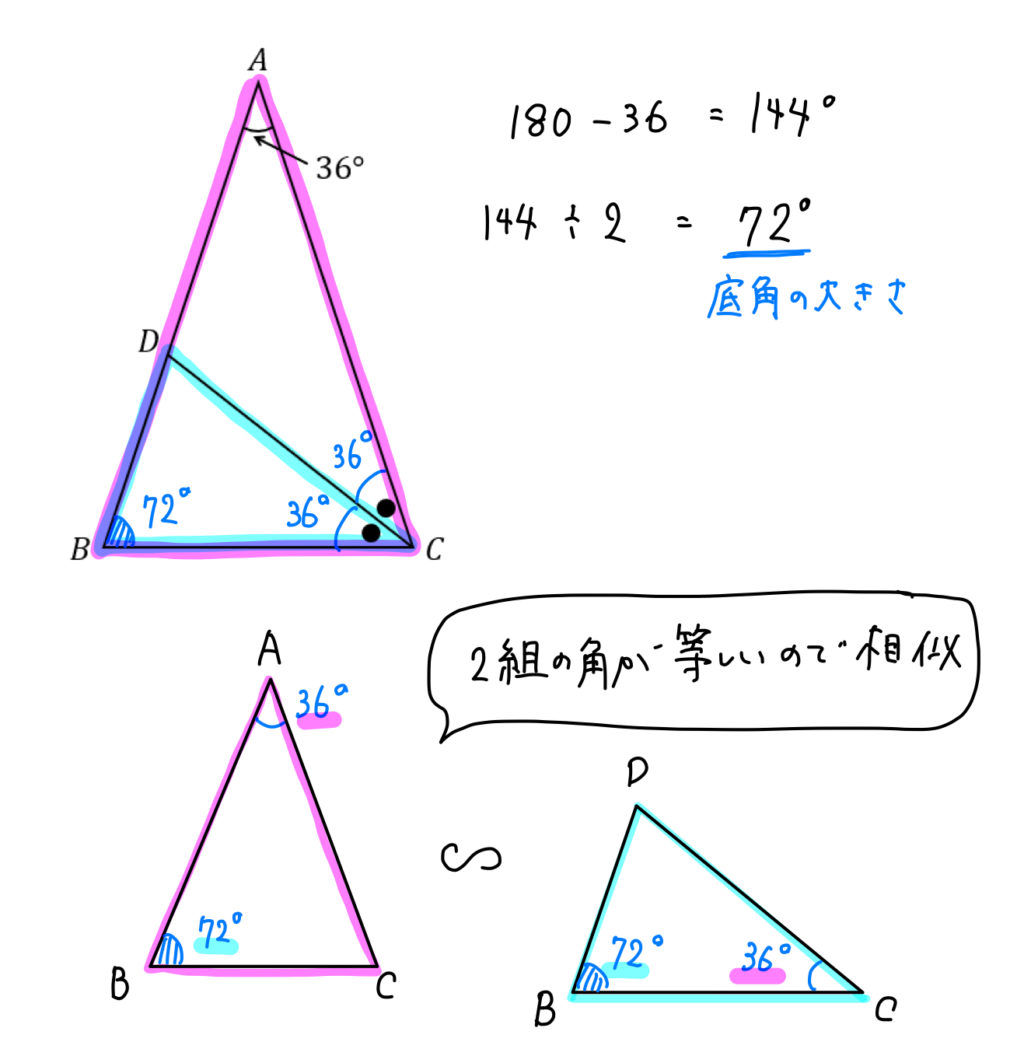
数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ

三角比15ºと75º 数式で独楽する

スタディピア 図形

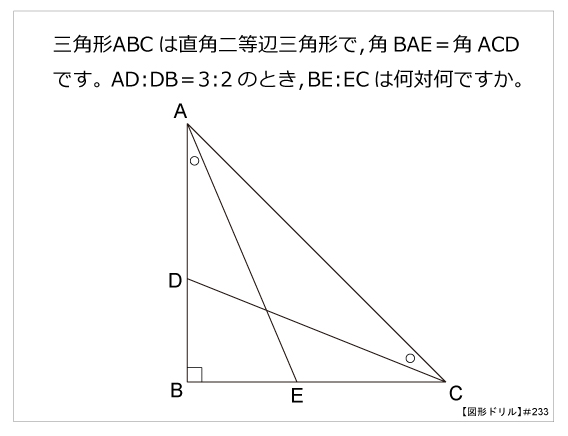
第233問 直角二等辺の辺の比 図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

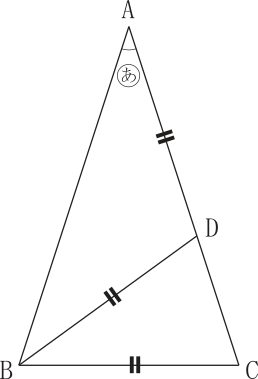
二等辺三角形 In 二等辺三角形 角度の問題 算数の広場

Math Battle 0075 一辺を共有する二等辺三角形

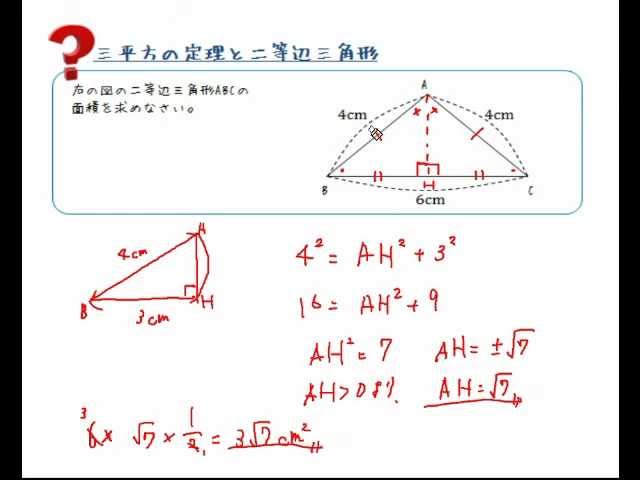
三平方の定理と二等辺三角形 Youtube

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo